Introduction

Efficient wellbore cleaning is an important goal in a drilling operation especially in horizontal and deviated wells since it can prevent problems such as stuck pipe, lost circulation, high torque and drag, loss of control on density ECDs, and finally it can reduce the cost of the drilling operations (Ozbayoglu et al. 2003). Some of affective parameters on wellbore cleaning have been studied by some researchers experimentally (Tomren et al. 1986; Yu et al. 2004; Ford et al. 1990; Hareland et al. 1993; Okrajni and Azar 1986; Sifferman and Becker 1992; Hussaini and Azar 1983) and by modeling approach (Nguyen and Rahman 1998; Wazed 2002; Akhshik et al. 2015; Zhu et al. 2013).

Tomren et al. (1986) published the results of experimental studies with various drilling fluids in plastic pipe lines with inclination angle from 0° to 90°. They stated that for a constant mud flow rate cutting bed thickness increased by increasing inclination angle. Also, they called the angle between 40° and 50° as critical angle since cutting bed thickness is formed and cuttings are slipped on the cutting bed in the critical angle. Ford et al. (1990) studied drilling cutting transport in deviated wells. They used a pipe line with 9 ft length, inclination angle from 0° to 90° and 3.5 in. internal diameter. The results of their work showed that flow regime and rheological properties of the drilling fluid are the key parameters in well cleaning operation and water with turbulence flow has a good performance in well cleaning. Horeland et al. (1993) investigated lime cutting transport in water base mud and invert emulsion oil base mud. They stated that for both muds with same rheological properties, water base mud has a better performance in the wells with 40°–50° inclination. Okrajni and Azar (1986) examined the effect of mud rheology on the annulus cleaning. The result of their experiments showed that mud rheology properties have a low effect on the cutting transport in turbulence flow, and in laminar flow, cutting transport is done better by increasing mud yield point. Sifferman and Becker (1992) accomplished a set of cutting transport experiments in deviated wells with deviation angle from 45° to 90°. They investigated the effect of various parameters on cutting transport such as drilling fluid velocity, density and rheological properties of mud, mud type, cutting size, ROP, RPM, drill pipe eccentricity, drilling pipe diameter and well angle. Based on their experiments, velocity and mud density are the most effective parameters on the well cleaning. Also, formed drilling cuttings beds make a slop from 45° to 60° in which they make slippage of cutting on the bed. Shadizadeh and Zoveidavianpoor (2012) carried out experiments for the investigation of the effect of various parameters on well cleaning in the lowest possible velocity of cutting transport and compared their model with Larsen numerical model (Larsen et al. 1997). They expressed that well angle is the most effective parameter in the well cleaning, and the worse condition of cutting transport is observed at 70°.

An advanced trilayers mechanical model was presented by Nguyen and Rahman (1998). Nonetheless, the application of this model is not proved by experimental results. They studied the effect of physical properties of cuttings, drilling fluid and drill pipe eccentricity on the cutting transport. Wazed (2002) investigated affecting parameters on the cutting transport in vertical and horizontal wells by CFD and compared the results of modeling with the results of experimental work of Sifferman and Becker (1992). He stated that flow regime and geometrical shape between inner and outer pipes have an important effect on the cutting transport. Akhshik et al. (2015) examined drill pipe rotation effect on the cutting transport in horizontal and vertical wells by CFD-DEM numerical modeling. In this modeling, fluid and drilling cuttings are considered as continuous phase and non-continuous phase, respectively. Comparison between CFD-DEM model by Akhshik et al. (2015) and CFD model by Ozbayoglu et al. (2010) and also, mathematical equations by Yu et al. (2007) showed that CFD-DEM modeling has a better performance in modeling of cutting transport. Zhu et al. (2013) studied the cutting transport in horizontal wells by CFD modeling and Navier–Stokes equations and showed that the amount of formed cuttings considerably decreased by increasing fluid velocity. Uduak and Skalle (2012) used CFD modeling and experimental observations to find a mathematical relation for non-Newtonian fluid and turbulence flow in annulus. The results of their work showed that non-Newtonian fluid has a highest velocity compared to Newtonian fluid near the wall of the annulus in which this high velocity is necessary for proper cutting transport. Also, spherical shape cutting are transformed better compared to other cutting shapes in critical velocity.

Okpobiri and Ikoku (1986) presented a semiempirical relationship to determine the frictional pressure loss due to the solid phase in the foam flow. They see a frictional pressure loss with increasing solid volumetric rate at a fixed Reynolds number. Guo et al. (1995) investigated the bottom hole pressure with foam drilling and using equation of state for foam and assumed drilling cutting transport velocity is 1.5 ft/s at the bottom hole. They investigated the hydrostatical head in the annulus using iterative method and took foam as a power law fluid. Herzhaft (1999) investigated cutting transport with foam fluid and presented that increasing foam quality the cutting transport is increased. Bilgesu et al. (2002) simulated cutting transport with computational fluid dynamic and showed fluid velocity in annulus has an important effect on the cutting transport. Also, the cutting transport efficiency is increased in low flow rates for all muds with various density. In this study, various affecting parameters on the drilling cutting transport in horizontal wells have been investigated by simulation and numerical modeling approaches, and finally the results are validated by experimental results.

Although various affecting parameters on hole cleaning have been reported by some researchers during past decades (Tomren et al. 1986; Yu et al. 2004; Ford et al. 1990; Hareland et al. 1993; Okrajni and Azar 1986; Sifferman and Becker 1992; Hussaini and Azar 1983; Nguyen and Rahman 1998; Wazed 2002; Akhshik et al. 2015; Zhu et al. 2013), a comprehensive investigation of drilling fluid, cutting density, deposit ratio, string stress on the hole cleaning especially in horizontal wells has not been fully studied. Highlighting the contribution of the article, in this study various affecting parameters on hole cleaning in horizontal well by CFD simulator have been investigated and the results are verified with experimental data in literature.

Governing equations

This section presents the mathematical equations governing the problem and discusses their relationship with the physical values and phenomena. Given less computational time and no need to find the movement path of individual particles, as well as unimportance of the shape of interface between the two phases despite their relative movement, mix model was used in this research. In this study, the drilling fluid and the cuttings were considered to be the continuous phase and the only dispersed phase, respectively. The mix model equations were presented by different researchers in various forms. For example, Ishii (1975), Ungarish (1993) and Gidaspow (1994) each presented a mix model for multi-component two-phase fluid based on different applications. The model proposed by Ishii (1975) is discussed here. In this section, all of the required and applicable equations used in this study by CFD simulator are presented. The presented equations such as continuity equation, momentum equation and velocity equation, all are required for a comprehensive simulation and modeling.

Continuity equation for the mixture

Applying the law of mass conservation for phase k gives:

$$\frac{\partial }{\partial t}\left( {\alpha_{k} \rho_{k} } \right) + \nabla \cdot \left( {\alpha_{k} \rho_{k} u_{k} } \right) = \varGamma_{k}$$
(1)

where α k is the volume fraction of phase k and Γ k represents the rate of mass generation of phase k at the interface. Summation of Eq. (1) for all phases gives:

$$\frac{\partial }{\partial t}\mathop \sum \limits_{k = 1}^{n} \left( {\alpha_{k} \rho_{k} } \right) + \nabla \cdot \mathop \sum \limits_{k = 1}^{n} \left( {\alpha_{k} \rho_{k} u_{k} } \right) = \mathop \sum \limits_{k = 1}^{n} \varGamma_{k}$$
(2)

The right-hand side of the equation above is, in fact, the source term of the continuity equation and represents mass production by the reaction. Since no reaction is occurring in this problem, the right-hand side of Eq. (2) can be neglected. The mixture density, ρ m and mixture velocity, u m are defined as follows (c k is the mass fraction of phase k):

$$\rho_{m} = \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{k}$$
(3)
$$u_{m} = \frac{1}{{\rho_{m} }}\mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{k} u_{k} = \mathop \sum \limits_{k = 1}^{n} c_{k} u_{k} \;{\text{and}}\;c_{k} = \frac{{\alpha_{k} \rho_{k} }}{{\rho_{m} }}$$
(4)

According the equations above for mixture continuity, it can be written:

$$\frac{{\partial \rho_{m} }}{\partial t} + \nabla \cdot \left( {\rho_{m} u_{m} } \right) = 0$$
(5)

Since the drilling fluid under study was assumed to be incompressible, Eq. (5) can be simplified due to having constant densities.

$$\nabla \cdot \mathop \sum \limits_{k = 1}^{n} \alpha_{k} u_{k} = 0$$
(6)

Momentum equation for the mixture

Applying the law of mass conservation for each phase gives:

$$\frac{\partial }{\partial t}\left( {\alpha_{k} \rho_{k} u_{k} } \right) + \nabla \cdot \left( {\alpha_{k} \rho_{k} u_{k} u_{k} } \right) = - \alpha_{k} \nabla p_{k} + \nabla \cdot \left[ {\alpha_{k} \left( {\tau_{k} + \tau_{Tk} } \right)} \right] + \alpha_{k} \rho_{k} g + M_{k}$$
(7)

The momentum equation for the mixture is obtained by summing up the equations of all phases.

$$\frac{\partial }{\partial t}\mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{k} u_{k} + \nabla \cdot \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{k} u_{k} u_{k} = - \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \nabla p_{k} + \nabla \cdot \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \left( {\tau_{k} + \tau_{Tk} } \right) + \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{k} g + \mathop \sum \limits_{k = 1}^{n} M_{k}$$
(8)

Given the definitions for mixture velocity, density, and Eqs. (4) and (5), the second term of Eq. (8) can be written as:

$$\nabla \cdot \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{k} u_{k} u_{k} = \nabla \cdot \left( {\rho_{m} u_{m} u_{m} } \right) + \nabla \cdot \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho_{m} u_{mk} u_{mk}$$
(9)

where u mk represents diffusion velocity, i.e., the velocity of phase k relative to the mixture velocity.

$$u_{mk} = u_{k} - u_{m}$$
(10)

Considering the mixture quantities, Eq. (11) for momentum can be written as:

$$\frac{\partial }{\partial t}\rho_{m} u_{m} + \nabla \cdot \left( {\rho_{m} u_{m} u_{m} } \right) = - \nabla p_{m} + \nabla \cdot \left( {\tau_{m} + \tau_{Tm} } \right) + \nabla \cdot \tau_{Dm} + \rho_{m} g + M_{m}$$
(11)

The three stress tensors in Eq. (11) are defined as:

$$\tau_{m} = \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \tau_{k}$$
(12)
$$\tau_{Tm} = - \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \overline{{\rho u_{Fk} u_{Fk} }}$$
(13)
$$\tau_{Dm} = - \mathop \sum \limits_{k = 1}^{n} \alpha_{k} \rho u_{mk} u_{mk}$$
(14)

where τ m is average stress tensor, \(\tau_{Tm}\) is average turbulency stress and \(\tau_{Dm}\) is the stress caused by phase relative slippage. Given the physical conditions governing the problem and the high viscosity of the fluids used in this study, all flow regimes are laminar. Therefore, the turbulency stress was neglected. The mixture pressure is defined as:

$$\nabla p_{m} = \mathop \sum \limits_{k = 1}^{n} \alpha \nabla p_{k}$$
(15)

The last term of momentum equation is related to the interfacial tension, which was neglected in this case due to the presence of solid and liquid phases.

Phase conservation equation

Starting with conservation equation for a single-phase (Eq. (1)) and replacing the phase velocity on Eq. (10) with the diffusion velocity, the conservation equation for a single phase becomes:

$$\frac{\partial }{\partial t}\left( {\alpha_{k} \rho_{k} } \right) + \nabla \cdot \left( {\alpha_{k} \rho_{k} u_{m} } \right) = \varGamma_{k} - \nabla \cdot (\alpha_{k} \rho_{k} u_{mk} )$$
(16)

Assuming constant density and no phase change, the phase conservation equation reduces to:

$$\frac{\partial }{\partial t}\alpha_{k} + \nabla \cdot \left( {\alpha_{k} \rho_{k} u_{m} } \right) = - \nabla \cdot (\alpha_{k} \rho_{k} u_{mk} )$$
(17)

Slip velocity or relative velocity

Another type of velocity usually used in two-phase flows is slip velocity or relative velocity (u Ck ), which is calculated as the difference between the velocity of dispersed phase, k, and the continuous phase. The subscript “c” represents the continuous phase velocity, and u c represent the drilling fluid velocity. The subscript “k” also represents the dispersed phase velocity and u k represents the moving velocity of drilling cuttings (Schiller and Nauman 1933).

$$u_{Ck} = u_{k} - u_{c}$$
(18)

The phase diffusion velocity can be defined as a function of slip velocity:

$$u_{mk} = u_{Ck} - \mathop \sum \limits_{k = 1}^{n} c_{k} u_{Ck} \mathop {\longrightarrow}\limits^{{{\text{for}} \;{\text{a}}\;{\text{dispersed}}\;{\text{phase}}}} u_{mk} = (1 - c_{p} )u_{Ck}$$
(19)

Estimation of diffusion velocity

Before solving Eq. (16) for mass conservation and the mixture momentum conservation equation, the diffusion velocity, \(u_{mk}\) must be estimated. The phase diffusion velocity is a function of the density difference between the dispersed and continuous phase. The drag force is the most important force determining this velocity. In order to find a relationship to be used for estimating the diffusion velocity, one must begin with the law of mass conservation and momentum conservation for a single phase. Combining these two equations and assuming laminar flow, and no mass transfer between the phases, and constant density yields:

$$\alpha_{k} \rho_{k} \frac{{\partial u_{k} }}{\partial t} + \alpha_{k} \rho_{k} \left( {u_{k} \cdot \nabla } \right)u_{k} = - \alpha_{k} \nabla p_{k} + \nabla \cdot \left( {\alpha_{k} \tau_{k} } \right) + \alpha_{k} \rho_{k} g + M_{k}$$
(20)

Writing the same equation for the mixture and neglecting the interfacial tension for the mixture (M m  = 0) gives:

$$\rho_{m} \frac{{\partial u_{m} }}{\partial t} + \rho_{m} \left( {u_{m} \cdot \nabla } \right)u_{m} = - \nabla p_{m} + \nabla \cdot \left( {\tau_{m} + \tau_{Dm} } \right) + \rho_{k} g$$
(21)

Neglecting the pressure gradient in Eqs. (20) and (21) and combining them yields:

$$M_{k} = \alpha_{k} \left[ {\rho_{k} \frac{{\partial u_{mk} }}{\partial t} + (\rho_{k} - \rho_{m} )\frac{{\partial u_{m} }}{\partial t}} \right] + \alpha_{k} \left[ {\rho_{k} \left( {u_{k} \cdot \nabla } \right)u_{k} - \rho_{k} (u_{m} .\nabla )u_{m} } \right] - \nabla \cdot \alpha_{k} \tau_{k} + \alpha_{k} \nabla \cdot \left( {\tau_{m} + \tau_{Dm} } \right) - \alpha_{k} (\rho_{k} - \rho_{m} )g$$
(22)

Since the problem under study is steady state, the time derivative of the variables equals zero. So, the term “\(\frac{{\partial u_{Mk} }}{\partial t}\)” in the first bracket in the right-hand side can be neglected. Due to high viscosity of the fluids and small size of the cuttings in this study, the cutting and the fluid velocity can be assumed identical and, in fact, the drilling cuttings can be assumed to be floating in the drilling fluid. Assuming two-times greater velocity for the drilling cuttings and fluid, the approximation \(\left( {u_{k} \cdot \nabla } \right)u_{k} \approx \left( {u_{m} \cdot \nabla } \right)u_{m}\) was used in the second bracket of the right-hand side.

Another important point to be mentioned is that the magnitude of viscous stress is negligible compared to other terms of the momentum equation in most problems. It is only significant in case where the stress rate is so great that viscous loss will result in fluid heating. This occurs when the fluid viscosity is very high and the velocity gradient is significant. In this study, the viscous stresses were negligible compared to other terms. On the other hand, the momentum transfer between the phases can be expressed as a function of slip velocity. For laminar flow:

$$M_{k} = - \beta u_{Ck}$$
(23)

Ishii and Mishima (1984) proposed the following equation for beta coefficient:

$$\beta = \frac{3}{4}C_{D} \frac{{\alpha_{k} \rho_{k} \left| {u_{Ck} } \right|}}{{d_{p} }}$$
(24)

where d p is particle diameter, ρ l is liquid density and C D is elasticity modulus. According to the simplified Eqs. (22), (23) and (24):

$$\frac{1}{2}\rho_{l} A_{p} C_{D} u_{Ck} u_{Ck} = V_{p} (\rho_{k} - \rho_{M} )\left[ {g - \left( {u_{m} \cdot \nabla } \right)u_{m} - \frac{{\partial \rho_{l} }}{\partial t}} \right]$$
(25)

This approximation can now be used to estimate slip velocity. Given the steady-state flow:

$$u_{Ck} u_{Ck} = \frac{{V_{p} (\rho_{k} - \rho_{M} )\left[ {g - \left( {u_{m} \cdot \nabla } \right)u_{m} } \right]}}{{\frac{1}{2}\rho_{l} A_{p} C_{D} }}$$
(26)

The diffusion velocity can now be estimated using Eq. (19).

Elasticity modulus

Different equations have been proposed to estimate elasticity modulus. A common relationship for elasticity modulus is proposed by Schiller and Nauman (1933):

$$C_{D} = \left\{ {\begin{array}{*{20}l} {\frac{24}{Re}(1 + 0.15Re_{p}^{0.687} ),} \hfill & {Re_{p} < 1000} \hfill \\ {0.44,} \hfill & {Re_{\text{p}} \ge 0} \hfill \\ \end{array} } \right.$$
(27)

where \(Re_{p}\) is Reynold’s number of the particle and is calculated as:

$$Re_{p} = \frac{{\rho_{l} d_{p} u_{Ck} }}{{\mu_{l} }}$$
(28)

The Reynolds number in this study was about 1000, so the first term of Eq. (27) was used. Equation (27) is developed for elasticity modulus of a particle inside the fluid, but increasing particle concentration results in a greater resistance against movement of the particles in fluid. So, each particle undergoes a greater tension than the single state. One way to consider this increase in tension force is to modify the viscosity (Ishii and Mishima 1984). The equations proposed by Ishii and Zuber (1979) were used to calculate mixture viscosity. For a solid–liquid mixture, this equation is expresses as:

$$\mu_{m} = \mu_{l} \left( {1 - \frac{{\alpha_{k} }}{0.62}} \right)^{1.55}$$
(29)

where \(\mu_{l}\) is liquid viscosity calculated by the following equation:

$$\left\{ {\begin{array}{ll} {\mu_{l} = \frac{{\tau_{0} }}{{\dot{\gamma }_{{{\text{crit}}.}} }} + k\dot{\gamma }^{n - 1} , } &\quad {\dot{\gamma } > \dot{\gamma }_{{{\text{crit}}.}} } \hfill \\ {\mu_{l} = \frac{{\tau_{0} }}{{\dot{\gamma }_{{{\text{crit}}.}} }} + k\dot{\gamma }_{{{\text{crit}}.}}^{n - 1} ,} &\quad {\dot{\gamma } < \dot{\gamma }_{{{\text{crit}}.}} } \hfill \\ \end{array} } \right.$$
(30)

where \(\dot{\gamma }_{{{\text{crit}} .}}\) is the critical shear rate. The fluids used in simulation followed power law rheological model, defined as:

$$\tau = K\dot{\gamma }^{n}$$
(31)

Boundary conditions

Determining the boundary conditions is one of the most critical stages in different fluid dynamics calculation applications. The boundary conditions used in this study are briefly discussed in the following. The inlet boundary condition is used to define the velocity or mass flux of the flow with all scalar properties of the flow at inlet. The following parameters are determined at inlet boundary:

  • Flow velocity and direction.

  • Volumetric fraction of the drilling cuttings in the flow.

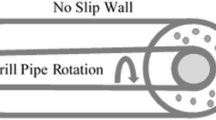
The inlet velocity can be specified by different ways, such as determining the velocity magnitude and direction or the velocity components. Flow outlet borders in these problems are positioned so that the flow development is guaranteed. Therefore, the development outlet condition, which implies a zero value for all gradients, except pressure along the annulus, is applied on the problem. Given drilling conditions and fixed wellbore walls in all cases simulated in this study, the outer wall of the annulus was simulated as a fixed wall. But due to the possibility of rotation of the drill string, the outer wall was considered to be fixed in some cases and with a constant rotational velocity along the annulus central axis in other cases. No-slip condition was applied on all walls.

CFD simulation

The behavior of drilling mud with cuttings in the annulus was studied via Fluent software for CFD simulation. Cutting transfer, mud cake thickness, mass fraction of cuttings in the mud cake, pressure drop and the shear stress exerted on the drill pipe were estimated. It has to be noted that based on the rheological studies, the power law model well-fitted the drilling fluid behavior, so it was used in drilling fluid simulation as it well justified and predicted its behavior. Oil and gas well drilling conditions change based on drilling depth. The wellbore and drilling pipe diameter decreases by increasing depth. A horizontal annulus was considered in this study. Figure 1 shows a schematic of the simulated well.

Fig. 1
figure 1

Wellbore simulated area

Full size image

Geometry

As it was mentioned earlier, the simulations were carried out for horizontal drilling. In horizontal drilling, the drilling bit deviates from the pipe center by its weight and moves down the wellbore. So, besides designing concentric drill string (eccentricity factor = 0), the results should be investigated for an eccentric bit in order to study the effect of drill string deviation from the annulus central axis. It has to be noted that the bit deviation from center is defined by the following equation:

$${\text{eccentricity}} = \frac{{{\text{distance }}\;{\text{between}}\; {\text{bit}}\;{\text{and}}\;{\text{bore}}\;{\text{center}}}}{{{\text{annulus }}\;{\text{thickness}}}}$$
(32)

Figure 2 shows the geometry created for concentric drill string, and Fig. 3 shows the geometry created for a drill string without concentricity with the annulus.

Fig. 2
figure 2

Annulus-drill string geometry created for concentric mode

Full size image
Fig. 3
figure 3

Annulus-drill string geometry created for eccentric mode

Full size image

Gridding

Finite volume method always starts with discretizing the flow region and associated transfer equations. The computational grid in this problem was created in a structured manner using Gambit software. Figure 4 shows the grids created on concentric annulus-drill string geometry in a horizontal cross section. In order to reduce error, the hexagonal grids were implemented on the well with cubic elements. It is clear from this figure that the cross section of computational grid is cubic in longitudinal and transverse directions. Because of great gradients of flow and concentration around the bit, the cells in that area were made finer to increase simulation accuracy. Figures 5 and 6 show the longitudinal cross section of the computational grid for concentric and eccentric cases, respectively.

Fig. 4
figure 4

Transverse cross section of the computational grid created on concentric annulus-drilling string geometry

Full size image
Fig. 5
figure 5

Longitudinal cross section of the computational grid created on concentric wellbore-bit geometry

Full size image
Fig. 6
figure 6

Longitudinal cross section of the network created on eccentric annulus-drill string geometry

Full size image

Since annulus-drill string geometry is not symmetrical in eccentric mode, applying structured grids results in a network with high dimensional ratio. Therefore, the computational network was crested as a pentaprism with triangular cross section. Figure 7 shows the transverse cross section of the network created.

Fig. 7
figure 7

Transverse cross section of the network created on eccentric annulus-drill string geometry

Full size image

Computational algorithm

The continuous phase equations were discretized using finite volume method, and the SIMPLEFootnote 1 algorithm was used to correlate the continuity and momentum equations.

According to the nature of diffusion phenomena, central difference method was used to solve the diffusion terms of the equations. The first-order upwind scheme was also used to estimate the magnitude of displacement terms in the momentum equations and volumetric fraction on the sides of computational cells. The equations governing fluid phase were solved numerically using the commercial software ANSYS Fluent v15.

Required information for simulation geometry

As it was mentioned earlier, oil and gas well drilling has different aspects according to the drilling depth, and the wellbore and drill string diameter decreases by increasing depth. The present study has examined a horizontal annulus with inner diameter, outer diameter and length of 4″, 8″ and 10′, respectively. Table 1 shows the dimensions and shape of the simulated well.

Table 1 Intermediate region characteristics of the simulated well located in Ahwaz oilfield
Full size table

Investigating the effect of eccentricity

In order to investigate the effect of weight in horizontal drilling, the deviation on the drill string must be examined as an effective parameter. Therefore, besides designing concentric drill string (eccentricity coefficient = 0), the results obtained for a bit with 0.62 eccentricity were studied to investigate the effect of drill string deviation from the annulus center. So, two eccentricity coefficients of 0 and 0.62 were studied.

Drilling fluid

The properties of drilling fluid and cuttings used in this study are reported in Tables 2 and 3, respectively. One of the parameters used in calculations was sphericity. Sphericity is an indicator of geometrical density. Since a sphere has the smallest surface among geometrical shapes of the same volume, the sphericity is calculated by comparing the surface of a geometrical shape with the surface of sphere having the same volume. Therefore, sphericity is defined as:

$${\text{sphericity}} = \frac{{{\text{surface}}\;{\text{area}}\;{\text{of}}\;{\text{an}}\;{\text{sphere}}\;{\text{with}}\;{\text{the}}\;{\text{same}}\;{\text{voulme}}}}{{{\text{surface}}\; {\text{area}}\;{\text{of}}\;{\text{the}}\;{\text{shape}}\;{\text{under}}\;{\text{study}}}}$$
(33)

Since the sphere surface area in minimum, the index defined above is a value in the range of (0, 1), and equals 1 for sphere.

Table 2 Rheological parameters of drilling mud
Full size table
Table 3 Cutting properties
Full size table

Operating conditions

The operating conditions used in the simulations are summarized in Table 4. It has to be noted that the volume fraction of the cuttings present at the annulus input was estimated by dividing the cuttings volume based on penetration rate over volumetric flow rate of the input fluid. Figure 8 shows the solving algorithm of the simulation.

Table 4 Operating conditions used in the simulations
Full size table
Fig. 8
figure 8

Solving algorithm of the simulation

Full size image

Results and discussion

This section discusses the simulation results and explains the effect of input parameters, including rotational speed of the drill string, drilling fluid and cuttings density, and deviation of the drill string from the annulus center, on precipitation of cutting, pressure drop of the drilling fluid and the stress exerted on the drill string.

Drilling process simulation

In drilling operations, the drilling is generally performed by rotation of drill string, and the formation drilled comes to the surface as solid cuttings. The drilling mud moves upward through the annulus as a result of injecting mud into the annulus and brings the cuttings up to the surface. Circulation of the drilling mud containing cuttings is affected by drill string rotation and injection rate. Figure 9 shows the velocity profile in a horizontal cross section of the annulus. It is clear from this figure that the velocity profile deviated from the uniform mode as a result of diffusion in the walls, and the velocity decreases in the vicinity of the walls. Since the fluid passing any cross section must be continuous based on the law of continuity, the velocity increases by increasing distance from the walls.

Fig. 9
figure 9

Velocity contour of drilling fluid in a horizontal cross section

Full size image

The important point to be noted here is that a downward velocity component forms for cuttings due to their gravity and higher density. Figure 10 shows two-phase velocity vectors. It can be seen that the cuttings tend to precipitate as a result of gravity and form a cutting film on the wall. The point to be noted in this figure is that the drilling mud flow becomes turbulent by precipitation of the cuttings, which in turn results in hydrodynamic complexity. It is also true for velocity vectors of the drilling mud, shown in Fig. 10b.

Fig. 10
figure 10

Velocity vectors in a vertical cross section for a phase velocity of the cuttings, b phase velocity of the drilling mud

Full size image

Due to the friction between wellbore and drill string, as well as the effect of cuttings on mud flow and viscosity in the drilling fluid, a pressure drop occurs in the flow of drilling mud and the fluid pressure decreases. It is well known that by increasing the fluid pressure drop, higher energy is required for mud pumping, and the metal mantle should also be more resistant. So, the pressure drop is a very important parameter in this context. Figure 11 shows pressure drop in a horizontal cross section. The point to be noted in this figure is that as the distance from mud injection point increases, the cuttings will have a greater tendency to move down the annulus due to cutting precipitation. This would increase the resistance against the fluid in the lower section and results in greater pressure drop in that area. It is evident that pressure drop in the lower section of pipe intensifies by increasing the distance from injection point.

Fig. 11
figure 11

Pressure contour in a horizontal cross section

Full size image

As it was mentioned earlier, the cutting precipitates due to the density difference between drilling fluid and cuttings and a cutting film forms on the lower wall. Cutting precipitation has a significant effect on velocity profile, pressure and, generally speaking, on the flow dynamics. In other words, cutting precipitation indicates the extent of efficiency of the drilling operation. The higher the amount of cuttings, the greater the cutting precipitation, i.e., the drilling mud carries less cuttings, and the cutting transfer system becomes less efficient. Figure 12 shows the fluid flow lines, and the line colors indicate the cuttings volume fraction. Volume fraction of the second phase is shown in Fig. 13. It is expected that the cuttings will precipitate and a mud cake will form on the wall. Volume fraction in vertical cross sections is shown in Fig. 14 to better understand the cuttings precipitation. It can be observed that the cuttings gradually precipitate and the drilling mud in the upper section is almost free of the cuttings, i.e., the cuttings are not carried in some parts of the mud. Another point to be noted is that the cuttings remain around the drill string by its rotation.

Fig. 12
figure 12

Flow lines colored based on cuttings volume fraction

Full size image
Fig. 13
figure 13

Volume fraction of the cuttings in a horizontal cross section

Full size image
Fig. 14
figure 14figure 14figure 14

Cuttings volume fraction along a longitudinal cross section of the annulus in terms of distance from the input section: a 0″, b 12″, c 24″, d 36″, e 48″, f 60″, g 72, h 48″, i 96″, j 108″, k 120″ (output)

Full size image

It can be argued that floating of the cuttings in the drilling mud is the result of two factors: the gravity force, which results in precipitation of the cuttings, and the drill string rotation, which has an opposite effect and prevents precipitation of the cuttings by circulating the drilling mud. It is known that the momentum effects of the drill string decreases by increasing the distance from it, while the weight force is bulk and applies uniformly to the whole fluid. Therefore, it is expected that the rate of cuttings precipitation will increase by increasing distance from the drill string as the weight force in constant, but the effect of drill string rotation decreases.

This can also be seen by comparing the cuttings volume fraction shown in Fig. 14. Cutting precipitation occurs faster at the annulus input (Fig. 14a) up to 48″ distance (Fig. 14e), where the cuttings are located at a greater distance from the drill string. But the cuttings slowly precipitate in the upper section of the annulus, so that the precipitation decreases from 48″ distance (Fig. 14f) up to 84″ distance (Fig. 14h), and no precipitation occurs at the ending part [from 84″ distance (Fig. 14e) to end part of the annulus (Fig. 14j)].

The 3D view of cuttings distribution is shown in Fig. 15. The cuttings distribution are cleary shown in this figure. As it was expected, the cutting gradually precipitates due to density difference with the mud, and the drilling fluid free from cuttings passes over the drill string, while the cuttings concentration increases at the lower section of the drill string. This phenomenon is unfavorable for a number of reasons. First, one of the most important functions of the drilling fluid is to carry the cuttings outside the annulus, but the fluid in the upper section of the drill string, which is free from the cuttings, is unable to do so. On the other hand, precipitation of the cuttings to the lower section increases the mixture viscosity in this section and results in higher pressure loss, which, in turn, requires more power to carry out the cuttings in this area. Moreover, the injection fluid chooses the upper path due to less pressure drop. Therefore, carrying the cuttings would not be performed efficiently in the lower section of the annulus.

Fig. 15
figure 15

3D view of cuttings distribution in the annulus

Full size image

Investigating the effect if drilling fluid density

Mud density is one of the most important parameters in drilling operations. Higher density requires more power for mud pumping. On the other hand, it makes carrying the cuttings easier. Since the quantitative value of density is intangible, the dimensionless density, shown by ρf, which is obtained by dividing the density over the operational density value, is usually used in the simulation. The following discusses the quantitative effects of drilling fluid density in the system performance.

Investigating the effect of drilling fluid density on pressure drop

It can be observed that the fluid pressure drop increases by resistance against fluid flow. It is clear from Fig. 16 that the fluid pressure drop increases by drilling mud density, so higher power will be required for mud pumping.

Fig. 16
figure 16

Pressure drop of the fluid in the annulus versus drilling mud density

Full size image

Investigating the effect of drilling fluid density on cutting precipitation

Figure 17 shows cutting precipitation versus fluid density. It can be observed that the cutting precipitation decreases by increasing fluid density as the density difference between cuttings and the fluid decreases and, in fact, the mixture tends to be more like a single-phase fluid, i.e., the gravity force applied on the drilling fluid and the cuttings becomes more close to each other.

Fig. 17
figure 17

Cutting precipitation in the annulus versus drilling mud density

Full size image

Investigating the effect of drilling fluid density on the stress applied on the drill string

The stress applied on the drill string is shear stress and is affected by the viscous effects of the drilling mud. This stress is a function of two general factors: fluid resistance against drill string movement and the drill string rotational speed. The fluid viscosity is affected by the amount of cuttings present in it. The more the cuttings present in the drilling fluid, the higher the viscosity. In fact, less cutting precipitation results in higher viscosity. Therefore, it is expected that there would be a direct relationship between drilling mud density and the stress applied on the drill string. Figure 18 shows the stress applied on the drill string versus fluid density. The point to be mentioned here is that the curve has an upward concavity, which implies a direct relationship between stress increment rate and the density, the reason of which is that more cuttings remain in the mud by increasing density, i.e., total viscosity increases. This is true for densities lower than operational density. Although the stress maintains its rising trend by increasing density to values higher than the operational density, the rate of applied stress decreases.

Fig. 18
figure 18

Stress applied on the drill string versus drilling mud density

Full size image

Investigating the effect of drilling cutting density

Cutting density is another important operational parameter influenced by the formation texture and soil compaction and composition. Generally, higher density of the cutting results in greater precipitation and more pressure drop due to cutting resistance against mud flow. The effect of cutting density on drilling operation is discussed in the following. Just like previous section, the ratio of cutting density to operation density of the cuttings, shown as ρparticle, is used for better perception of the value of cutting density.

Investigating the effect of drilling cutting density on pressure drop

As it was mentioned earlier, increasing cutting density increases their stability in the drilling mud due to increasing the density difference. This results in increasing the drag force applied between the phases and increasing the fluid flow pressure drop. Figure 19 shows the pressure drop versus cutting density. It is clear from this figure that the pressure drop increases by increasing cutting density. It is worth mentioning that due to the increase in cutting precipitation, the drilling fluid and cuttings actually get separated and there will be less pressure drop. In other words, the rising trend of pressure drop gradually decreases by increasing cutting density.

Fig. 19
figure 19

Drilling fluid pressure drop versus cutting density

Full size image

It has to be noted that the rate of pressure drop decreases by increasing cutting density, i.e., pressure drop will have a decreasing trend, the reason of which is that the density difference between the drilling fluid and cuttings increases by increasing cutting density, and the cutting will have a greater tendency to precipitate, i.e., cutting dispersion in the mud decreases and the fluid behavior will have a greater deviation from a single-phase fluid. In fact, there will be a more dilute fluid present along the path, which reduces the pressure drop. Equation 34 depicts the relationship between pressure drop and cutting density. The correlation coefficient for the equation proposed in this case is greater than 98%, which implies the accuracy of the equation

$$\Delta P = - 00.0052\rho_{\text{particle}}^{2} + 0.0159\rho_{\text{particle}} + 0.0577$$
(34)

Investigating the effect of drilling cutting density on precipitation

Figure 20 shows the drilling cutting density versus cutting precipitation. It is clear from this figure that the cuttings precipitation increase by their density, the reason for which is the increase in the density difference between the two phases, which increases the gravity force applied on the cuttings and yields in more precipitation.

Fig. 20
figure 20

Cutting precipitation versus cutting density

Full size image

Investigating the effect of cutting density on the stress applied on the drill string

The stress applied on the drill string was studied under different cutting densities. By increasing cutting density, they tend to precipitate more, and the fluid will no longer be a mixture of mud cutting, i.e., there will be a low-viscosity fluid at the upper section of the drill string, which reduces the stress applied on this section. On the other hand, cutting accumulation in the lower section makes this part to be engaged with a high viscosity fluid, which increases the stress applied on the drill string in this area. Therefore, it is expected that the stress applied on the drill string be subjected to two countercurrent factors and its behavior be subjected to some changes. Figure 21 shows the stress applied on the drill string versus cutting density.

Fig. 21
figure 21

Stress applied on the drill string versus cutting density

Full size image

Verification of the results by experimental tests

One of the most important stages performed in numerical simulations is verification of the results and examining the model accuracy. It is known that experimental tests are applicable under very limited conditions. Moreover, not all the variables can be deduced by them. On the other hand, analytical solution of differential equations is not feasible in complex geometries; therefore, implementing numerical methods is inevitable. However, in order to have reliable results, it is necessary to verify the data obtained with a more reliable method.

In current study, Eq. (35) was used for verification. This equation implies that pressure drop in a pipe is proportional to the ratio of stress applied on the drill pipe over drill pipe diameter.

$$\frac{\Delta P}{L} = \frac{{4\tau_{w} }}{D}$$
(35)

This equation is based on numerical solution and is obtained for a power law fluid with yield stress. Since the yield stress plays no role a flowing fluid, the equation above is true for power law fluids as well. Rearranging the equation above gives:

$$\frac{\Delta P*D}{{L*\tau_{w} }} = 4$$
(36)

The dimensionless parameter in the equation above was calculated at three points, and the results were compared with each other. The error was estimated by dividing the difference between the dimensionless parameter and 4 over the analytical value. Since the hydrodynamic field changes by changing density, the data associated with the drill string rotational speed were used for verification in order to estimate the error. Furthermore, since simulation was performed symmetrically, radius was used instead of diameter. It is clear that the simulation error is in the range of 0–20% (Table 5), which is acceptable for numerical simulations. Based on the Eq. (36), theoretically, the left side of the equation should be constant. To this end for a pipe with constant length and diameter, this dimensionless ratio is calculated at three points for pressure drop and shear stress. The results are compared with experimental data presented by Jiimaa (2014), and error percentage is presented in Table 5.

Table 5 Simulation error % (reproduced with permission from Jiimaa 2014)
Full size table

The major cause of error in the simulations is the difference between the assumptions made in analytical and numerical solution. In analytical solution, it was assumed to have yield stress and Herschel–Bulkley fluid, while the power law fluid was used in the simulation. Moreover, the fluid was assumed to be quasi-homogeneous in analytical solution, and the effect of cutting dispersion was also neglected. For verification, we only reported the dimensionless Eq. (36), because it is a good relation for verification. To this end, the verification results are presented at the end of the paper to show the accuracy of the whole CFD simulation. The results of validation show a good precision of the modeling.

Conclusions

In this study, various affecting parameters on the cutting transport in horizontal wells were investigated by CFD modeling. Also, a systematic validation study is done by experimental data against modeling results. The following results can be concluded:

  • Higher cutting density leads to higher cutting precipitation and more pressure drop due to more resistance against mud flow by denser drilling cuttings.

  • There will be a low-viscosity fluid at upper section of the drill string, which reduces the stress applied on this section. On the other hand, cutting accumulation in the lower section makes this part to be engaged with a high viscosity fluid which increases the stress applied on the drill string in this area.

  • The important point to be noted is that a downward velocity component forms for cuttings due to their gravity and higher density and cuttings tend to precipitate as a result of gravity and form a cutting film on the wall.

  • The rate of pressure drop decreases by increasing cutting density, i.e., pressure drop will have a decreasing trend, the reason of which is that the density difference between the drilling fluid and cuttings increases by increasing cutting density, and the cutting will have a greater tendency to precipitate. On the other hand, cutting density in the mud decreases and the fluid behavior will have a greater deviation from a single-phase fluid.

  • Cutting precipitation decreases by increasing fluid density as the density difference between cutting and fluid decreases. In fact the mixture tends to be more like a single-phase fluid, i.e., the gravity force applied on the drilling fluid and the cuttings becomes more close to each other.

  • The stress applied on the drill string is shear stress and is affected by the viscous effects of the drilling mud. The fluid viscosity is affected by the amount of cuttings present in the fluid. The more the cuttings present in the drilling fluid, the higher the viscosity result in increasing stress on the drilling string.

  • Increasing cutting density increases their stability in the drilling mud due to increasing the density difference. This results in increasing the drag force applied between the phases and increasing the fluid flow pressure drop as a result.

  • The results showed that by increasing two times of drilling fluid density/operational density, cutting precipitation ratio decreased 32.9% and stress applied on the drilling string and pressure drop increased 4.59 and 5.97%, respectively. By increasing two times of drilling cutting density/operational density, cutting precipitation ratio increased 200%. Also, there is an optimum point for drilling cutting density at 8.5 in which stress applied on the drilling string will be minimum.